When can dispersal synchronize populations?

March 9, 2017 michelle

Goldwyn, Eli E., and Alan Hastings. “When Can Dispersal Synchronize Populations?” Theoretical Population Biology 73, no. 3 (May 2008): 395–402. doi:10.1016/j.tpb.2007.11.012.

Synchrony has been observed in many ecological systems, including predator-prey and disease dynamics, and is thought to be driven by either exogenous or endogenous factors. Goldwyn and Hastings (2008) focus on the ability of one endogenous factor, dispersal, to lead to coupled oscillations between predator-prey populations. Theoretical studies have determined that there are several ‘pathways’ by which dispersal can lead to synchrony: extremely long periods between disturbances, high rates of dispersal over space, or autocorrelation matching that of environmental noise (Moran effect). The authors explore another pathway in this paper, the case in which a system is a relaxation oscillator, allowing fast convergence to synchronous dynamics. A relaxation oscillator arises when the dynamics of the organisms take place on different timescales, and is characterized by population outbreaks over a short time interval, with long periods of low populations in between (this is sometimes compared to a a blinking light).

Goldwyn and Hastings create a two-patch predator-prey model to explore the ability of a relaxation oscillator to converge on synchrony in a short time scale, as seen in nature. In the model, the prey has a fast time scale, and the predator a slower time scale, and the patches are coupled by a complementary (equal) dispersal parameter between patches. Through some complex (for this reader, at least) mathematics, they nondemensionalize a set of ODE’s to the timescale of the predation rate and derive a system of phase equations from the resulting coupled ODE’s of the patches, which allows them to focus on the difference in phase between the two patches, a measure of synchrony.

To explore the effect of predator vs. prey timescales, they alter several parameters to increase this ratio (leading to larger timescale differences), and find that the system becomes a relaxation oscillator in all cases. An increase in the timescale difference also leads to a faster convergence time, and affects a systems response to a perturbation. At similar timescales, a system is generally more sensitive to perturbation at all times, however as the timescales become more different, this sensitive becomes more peaked, and is highly sensitive if a perturbation occurs at a specific time, which, in this model, corresponds to time periods where the prey population is small. When the timescales are similar, the steady states are either synchronous and stable or anti synchronous and unstable, a result of bifurcations, however increasing the difference leads to two stable states, both synchronous and asynchronous, in addition to an unstable asynchronous steady state.

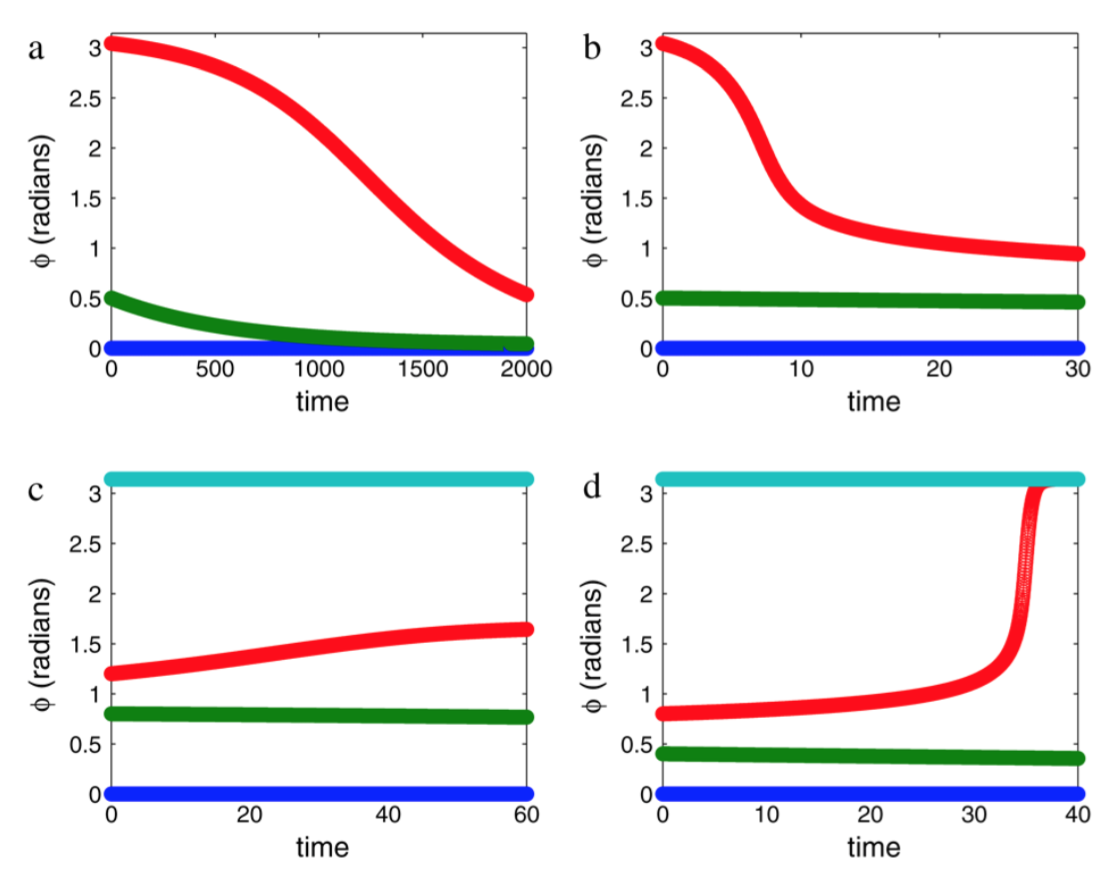
A plot of convergence patterns over time for systems with large differences in timescales (a & b) and similar timescales(c & d) for four initial starting conditions each. Note that a & b tend to converge towards synchrony (phi=0), though at different rates

The main finding from this study is that weak dispersal does not always mean a slow convergence on synchrony, and that the an increase in the difference in timescales of predator and prey can lead to rapid convergence to synchrony. Examples of this phenomenon do exist in nature, the most infamous being the spruce budworm outbreak example. A further conclusion to draw from this is that predator-prey dynamics that exhibit synchrony, but do not exhibit relaxation oscillations are most likely not synchronous because of weak dispersal, but as a consequence of strong dispersal or environmental cycling, such as the Moran effect.