Global asymptotic coherence in discrete dynamical systems

February 16, 2017February 16, 2017 paige Paige Miller

Earn, David JD, and Simon A. Levin. “Global asymptotic coherence in discrete dynamical systems.” Proceedings of the National Academy of Sciences of the United States of America 103, no. 11 (2006): 3968-3971.

http://www.pnas.org/content/103/11/3968.short

Synchrony is important in a number of settings including epidemiology, neurobiology, economics, engineering, and social sciences. In ecology, if a species has a low population density everywhere at the same time then rescue effects are unlikely to cause population recovery. Earn et al. (2000) showed general conditions where conservation corridors might actually cause extinction to be more likely in populations due to synchrony among the patches. In their numerical approach, they simulated population dynamics in a metapopulation of 10 patches, each with logistic population growth. Using two types of dispersal functions between patches, equal and nearest-neighbor coupling, they described regions of the parameter space where coherence is impossible, possible, and inevitable using an anlytical approach. These coherence conditions gathered from their analytical study were described in brief but derivation details were largely left to Earn & Levin (2006).

This paper described the derivation for global asymptotic coherence condition in detail. To derive these conditions, they studied a coupled map lattice (CML) because it is a simple framework for investigation. The CML does not need to be for a single species, it can be for any number of species (X^N). A CML is built from discrete maps such as the logistic map. There is a connectivity matrix (M) that describes the relationship between each lattice point (x_i). Through time, each species will have some density trajectory in each lattice point according to dispersal and reproduction. A coherent state is when each lattice point has the same number of some species at time=t. A coherent solution is when each lattice point has the same number of some species at all times t. To mathematically describe the conditions that give rise to coherence, they look for eigenvectors and then study if the population trajectory goes to zero or not. An eigenvector for a single population is just a vector of 1s which is n-dimensional (n=number of patches). But for meta-CMLs (many species CML) the eigenvector is a the unit vector (each element is divided by n). The vector of each species state space multipled by the unit eigenvector can be broken down to describe when a metapopulation relaxes to coherence: if the absolute value of the difference between the state of each patch minus the average state of each patch multipled by the unit eigenvector goes to zero as t goes to infinity. If this number does not go to zero, then the metapopulation is defined as asymptotically incoherent.

Paragraph describing their mathematical definitions of coherent and incoherent. e is the eigenvector for the trajectory.

From these mathematical definitions, they briefly outline some key elements of the local results to give context the global coherence condition. They say the theory is complicated but that local stability can be described in rough terms through the three parameters introduced in Earn et al. (2000). Local stability depends on the magnitude of the subdominant eigenvalue of the connectivity matrix and the maximum Lyapunov characteristic exponent of the full map describing state of all species in all patches.

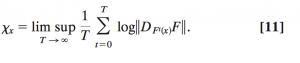
Definition of Lyapunov exponent which describes rate of divergence of patches from each other. T is the number of time steps. Sup means supremum (basically the maximum). D is determinant of the Jacobian.

The condition for coherence impossibility is when the log of the absolute value of the eigenvalue plus the Lyapunov exponent is greater than zero (meaning that all coherent points lie very close to incoherent trajectories and will move towards incoherence). The condition for coherence possibility means that most coherent points are close enough to coherent surfaces in the parameter space to have coherence possibility.

To describe the characteristics for global asymptotic coherence (GAC) they first examine the simplest case of a two patch system. The change in each patch can be simply calculated because movement from the other patch and the growth within the patch are the only things changing. From calculating the change in each patch they come to the conclusion that the absolute value of the sum of the migration probabilities subracted from one multipled by r has to be less than one for GAC. If they ignore the case of the baseic two patch system and the case of no connectivity between the two patches, they can derive an even more general condition of GAC: if the absolute value of the sub-dominant eigenvalue (of M) multiplied by r is less than 1. To prove their theorem they formulate a theorem and two lemmas. Their theorem allows them to say that if r<1, the full map F has a globally asymptotically stable fixed point. Then, they say that this fixed point is coherent under their condition. This paper was a difficult read, and even more difficult to understand, but it is a good example of an analytical solution that is generalizable to other dynamical systems. I would recommend skimming it to get a sense of the difficulties that analytical solutions represent.