Coupling Within-Host and Between-Host Infectious Diseases Models
Martcheva, Maia, Necibe Tuncer, and Colette St Mary. “Coupling Within-Host and Between-Host Infectious Diseases Models.” BIOMATH 4.2 (2015): 1510091.
The paper is a review of different models linking the within-host dynamics to the between-host processes. They begin by discussing within-host models. These dynamical models are used to represent the interaction between a pathogen and the replication machinery in the host or the immune responses of a host. They first present a within-host model of the pathogen replication cycle which assume that a viral pathogen replicates using target cells in the host.

This is similar to the model we used in class. x is the number of susceptible target cells, y is the number of infected target cells and P is the number of free pathogens. We can see that it has two equilibria: the disease free equilibrium (r/mu, 0, 0) and the “endemic”/”infection” equilibrium (x*, y*, P*).
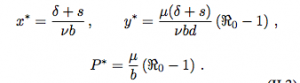

R0 is the reproduction number of the pathogen.
They then move to models with an immune response. The system of equations describing this interaction is:
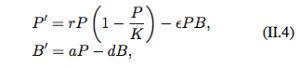
Now, the pathogen (P) replicates according to the logistic growth model and the production of the immune response depends on the abundance of the pathogen. These models also have two equilibria: the extinction equilbria which is unstable (0,0) and the coexistence equilibria (P*, B*).
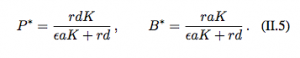
They then move to immuno-epidemiological models that link the within-host disease processes are interlinked to population-level dynamical models of disease spread. The start with network epidemic models. In these models, individuals are represented as nodes, which undergo within-host dynamics. These models are useful at understanding how individual dynamics in immune dynamics can influence population dynamics. However, popluation measure of disease dynamics (such as the reproductive number of the parasite and the prevalence) are impossible to analytically derive.
ODE immuno-epidemiological models allow for the derivation of these quantities assuming that the within-host dynamics are at equilibrium. These allow us to investigate how the within-host parameters, pathogen load and immune response can influence epidemiological quantities. However, these models are unrealistic as they assume that all individuals are identical and undergo the same within-host dynamics.
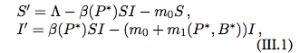
Size-structured PDE immuno-epidemiological models use physiologically structured PDEs in which the structural independent variables are the dynamical variables of the ODE immune model. Nested models are advantagous to these size-structured models as they allow for the use of very realistic and specific to a given disease model. There are only two independent variables in the PDE portion of the model there are vey few computational problems with these models.
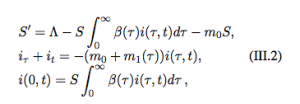
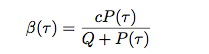
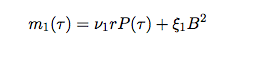
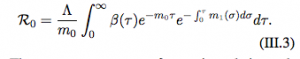
The reproductive number of pathogen depends on the within host parameters.
