Self-organized wave pattern in a predator-prey model.
Sun, Gui-Quan, et al. “Self-organized wave pattern in a predator-prey model.” Nonlinear Dynamics 60.3 (2010): 265-275.
The paper investigates the formation of spatial patterns (i.e. spiral waves) in a classical predator-prey system.
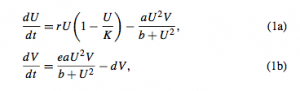
The authors develop a traditional Lotka-Volterra type predator-prey system with a Holling-III functional response. They assume that in the absence of predators, the prey will grow logistically. To convert the system into a set of partial differential equations (to incorporate space into their model), they write the system in system in a nondimensionalized form (to reduce the number of parameters) and then incorporated the spatial factor.

Next, they perform a linear stability analysis to determine if the steady states are stable in a spatially homogeneous system. The results show that: 1) the extinction of the predator and prey is always unstable 2) the extinction of only the predator is stable 3) the coexistence of the predator and prey is possible if specific parameter conditions are met.
Next, they perform a bifurcation analysis on the system. They find regions of homogenous stable equilibria, Hopf bifurcations and Turing bifurcations in parameter space A and D (figure 1 in paper).
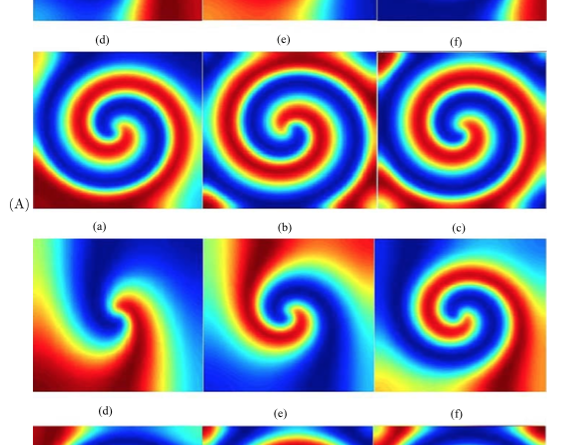
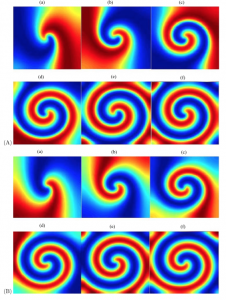
They then numerically simulated the system. First, they assumed a homogenous landscape and equal diffusion of the predator and prey with set parameter values that would result in a stable limit cycle in a nonspatial model. This results in spiral waves forming on the landscape (figure below).
![]()
These spiral waves also formed on a heterogenous landscape. These results highlight that the formation of these waves are an emergent phenomena driven by the intrinsic mechanism rather than the heterogeneity of the landscape/environment. They also perform a stability of analysis of the spiral waves.
Overall, they found that when considering a system with equal diffusion of the predatory and prey, spiral waves can form on the landscape should parameter values be set such that stable limit cycles occur without a spatial factor. The authors close with a short discussion about two assumptions of the model: the equal diffusion of the predator and the prey; and the linear function describing the death of the predator.