Individual-based, stochastic models for metapopulations on the brink of extinction
Levin’s model describes the change in the proportion of occupied patches within a metapopulation as a function of rate of successful colonization of an empty patch, and the rate of extinction in an occupied patch. However, the population dynamics within each patch are not explicitly considered. Other models focus on the within-patch dynamics of a single patch, but do not explicitly model the broader metapopulation. Eriksson et al. (2013) create a stochastic individual-based model (IBM) of metapopulation dynamics using a metapopulation of a large, but finite number of patches. They then determine how stochastic population processes influence the distribution of individuals across patches, and determine under what conditions Levin’s model accurately depicts metapopulation dynamics. They do this in metapopulations nearing extinction (a type of bifurcation point), which due to the mathematic properties of systems approaching bifurcation points, reduces the complexity of the dynamics to a single set of variables.
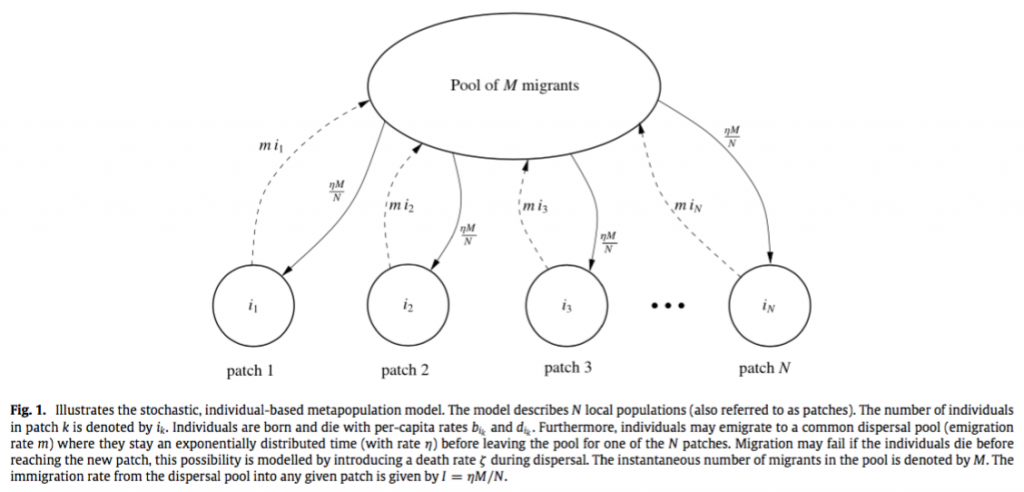
In their IBM, patches exhibit population dynamics of births, deaths, which are consistent across patches. Migration rates from a patch are proportional to the population size of the patch, and migrants go into the dispersal pool for a period of time until they reach their target patch, which is chosen from all the patches (which all have an equal probability of being chosen—Fig. 1). They use a master equation for the rate of change of the probability of observing a specific number of patches with a given number of individuals for solving for the state of the system (e.g. at equilibrium, or at specific time points). Under conditions of a very large number of patches, the stochastic fluctuations become essentially negligible, and the metapopulation dynamics can be described by the deterministic equation (Levin’s model). If the only steady state that can be solved for is when the fraction of patches with a set number of individuals is zero, then the metapopulation will go extinct. The authors demonstrate that the time to extinction depends on the demographic parameters r and K, as well as migration and the number of patches in the metapopulation.
- Eriksson, A., Elías-Wolff, F. & Mehlig, B. Metapopulation dynamics on the brink of extinction. Theoretical Population Biology 83, 101–122 (2013).
